|
|
| Re: t-SNE [message #1685 is a reply to message #1675] |
Tue, 19 July 2022 08:12   |
nbehrnd
Messages: 208
Registered: June 2019
|
Senior Member |
|
|
Sansun,
in a first approximation, you could determine the centres of gravity for each cluster, and from there the spread along (the projections of) x, y, z. You then could build a tetragonal parallelepiped of known dimension for each cluster and check if the volume one of these boxes is to some part enclosed by the box about the other cluster, if one cluster's box is totally enclosed by the box of the other (i.e., a sub-set of the space), or if the two are separate from each other.
The likely better approach were to perform a principal component analysis (PCA) to determine centre of gravity of each cluster, and to determine the corresponding eigenvectors. This would offer the advantage that the orientation of the vectors to construct an envelope of the cluster no longer is the projection along x, or y, or z, but that these vectors may have any orientation in space. (If you enter a 3D cluster each, I would constrain the PCA to only consider three dimensions.) PCA includes some vector transformation to centre (and normalize) the scattered clouds in first place; I do not recall if DW already is set up to perform these operations with a function from the GUI.
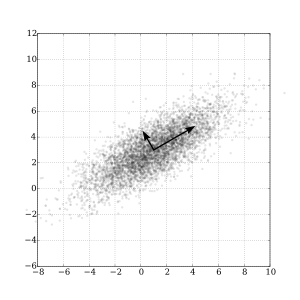
Norwid
image credit: https://en.wikipedia.org/wiki/Principal_component_analysis
|
|
|
|
| Re: t-SNE [message #1687 is a reply to message #1685] |
Tue, 19 July 2022 09:35 |
sansun
Messages: 45
Registered: April 2019
|
Member |
|
|
Hi Norwid
Thanks for the detailed response. I'll try that. I don't think it can be performed in DW though.
|
|
|
|
Search
Help
Members
Register
Login
Home
